Fluency Practice: Graphing Systems of Equations
Author’s note:
I wrote this lesson briefly the night before class (i.e., 1am–2:30am). Back when I was teaching, I had a rapid nightly routine of lesson-writing. It doesn’t take much to memorize the year’s standards and the example Pearson test questions that go with each. That memorization made it easy to see the overarching themes and connections between different topics.
In this case, though, I did have to take some extra time prior to get a sense of the Algebra curriculum, plus I did have my prerequisite argument with a few college classmates (math majors) regarding the efficacy of McGraw Hill’s lesson.
Typically, I never write lesson implementation guides. Given I didn’t have McGraw Hill when teaching (I generated my own curriculum nightly), there was no time to waste on formalizing retrospectives like this. But without this sort of guide/solutions/etc., it made it impossible to share my lessons with colleagues in the district—others who don’t know my students, don’t have my mathematical background, and don’t know how my class went yesterday. Since it’s Christmas break, though, I figured I’d take the time to write this up while it’s fresh in my mind.
I think this is a reasonable example for extending or supplanting a McGraw Hill lesson with application and drill at teacher discretion. Going through such an exercise is probably as (or more) effective as any framework for doing a lesson study prior to teaching something straight out of the adopted curriculum. Like I mention below, removing the cruft in an educated way is great for distilling both instructor and student goals and timing a lesson.
Please excuse any errors.
— Dhilan
Prologue
This week, I had the rare opportunity to follow up with my former seventh grade students and see their progress as they take on the world of Algebra. Here are some headline takeaways (only relevant to my work with the Algebra class) thinking back to their year of instruction (under my direction) just prior:
- As topics become increasingly involved and difficult, my students remain eager to learn. Applications are more-so a motivating force now as the students’ mathematical maturity improves. Distilling tough concepts like audio sampling or graphics scaling to proportionality in 7th grade worked fine, but 2D motion is a much more captivating usecase (as you’ll see in this lesson).
- Proficiency with fractions stinks. (This has not changed from last year despite lots of Kumon-esque drills.) Students continue to have a weak understanding the relationship between division and multiplication (reciprocals). But they also have a weak sense for scaling factors (including the effect of negatives), which was under my purview as a 7th grade standard.
- Strong students are motivated to stay on task when surrounded by other strong students. I’d never seen this at the scale of a whole class, but I was shocked to see this classroom’s overwhelmingly promising culture—of focus, independence (yet support for classmates), and a basal drive to understand.
- Connection from one year’s standards to the next year’s is weak if existing at all. I will take the blame for teach-to-the-test simplifications of techniques for solving equations; however, interestingly, when given an equation like $-\frac23x=2$ in the context of graphing, students were stuck attempting to apply the only thing they’ve seen this year (slope-intercept form) rather than doubling back to seventh grade ideas (isolating a variable as a first step to gain more intuition about an equation).
Lesson Goals
This lesson follows prior lessons on graphing inequalities. As such, we can expect prerequisite knowledge of graphing (via tabular methods and slope-intercept form which requires student recognition that they should solve for $y$). Graphing systems of equations reveals potential for intersection (or lack thereof) of two lines where a single solution, i.e., an ordered pair $(x,y)$, satisfies both provided equations. Students should:
- be able to graph two equations on one coordinate plane
- determine whether there exists a solution (an intersection)
- discover criteria for the case of no solution and infinite solutions
McGraw Hill emphasizes vocabulary (interestingly missing from TN Instructional Focus Documents) of “consistent” and “inconsistent” as well as “dependent” and “independent” which are useful in Linear Algebra, maybe, but provide little insight to the cases of grade-school Algebra. The link to foundational knowledge is too tenuous.
Instructor Goals
It is difficult, out of context, to motivate why finding a solution to a system is useful (outside the context of word problems establishing the two equations and their relationship). This inspires a use of an application of intersection to warm up the concept before deeper equation-to-scenario relationships in more involved problems (end-to-end from writing equations to solving the system) can be established. Avoid a “just do this and we’ll talk about why it’s useful later” attitude, time permitting 😆
Guided Worksheet
It’s worth noting: students are increasingly more capable of taking and organizing their own notes and work. (This was the expectation when I was in 8th grade Algebra.) That said, my default mode of operation is creating a worksheet for two reasons:- it forces me to think deeply about the flow of the lesson and cut the excess (curriculum writers include some of the most trivial nonsense which adds nothing to students’ intuition or fundamentals—I’m sure many writers spent years in the classroom, but they didn’t spend them in my inclusion classroom with 33% special ed students and a similar percent of ELL students)
- strictly limiting oneself to a single 8.5x11 paper works unbelievably well for perfectly pacing a one hour lesson
The exit ticket should be more sensible for a real class. I was visiting my students, so I just wanted to keep the lesson light so I could give myself time to chat with everyone (and make sure their attitude about Algebra is in-check).
Lesson Flow
Opener
Providing multiple bellringers (1) keeps students occupied, (2) offers an opportunity for a mini-lesson building up a concept from earlier to later bellringers in the series, and (3) provides multiple options of entrypoint for a student who may be stuck on one concept (students raising hands and queuing at the beginning of class is untennable for a teacher who has to complete administrative tasks, first).Because the lesson follows-on from graphing inequalities (and because the rest of the lesson relies so heavily on graphing), reviewing fundamentals in the context of their prior lesson is crucial. Not to mention, it serves as reference notes for the rest of the lesson. For a student that may have missed the prior lesson, this offers an opportunity to catch up.
- Students struggle with $x=4y-24 \rightarrow y = \frac{x}{4}+6$ since the final division affects two terms. When discussing as a group, ask the student who demoed their work what $m$ (the slope) would be for this problem to drive home the equivalence of division and multiplying by the reciprocal (multiplicative inverses).
- We saw students get to the final solution for $x \leq 3y-9$, graphing the inequality, but deciding whether to shade “above” or “below” was confusing to some who pre-determined that choice (i.e., shading below because the original had $\leq$) before getting to slope-intercept form $\rightarrow$ motivates checking a solution. Extending the problem with a quick followup (switching sign and inclusivity) not meant for further algebraic manipulation should test students’ intuition.
Vocabulary
I, notoriously, hate math vocabulary (but succumb to some pressure after talking to my college classmates who are staunch advocates for foundational vocab). I thought, as a nice twist, it could be cool to use some Boolean logic to explain no solution (inconsistent) and a riddle to explain one solution:- Mr. R cannot be and not be something at the same time. (Note: students are creative and come up with a workaround for words with two meanings…kids are mean.)
- A clock has two arms but no feet. I did think that was the only solution, but of course (I wish I had 8th grade creativity), an “amputee” can fit the category, too 🙃
DVD Logo Exercise (Concept Application)
Linear equations offer an infinite number of applications. But finding the right ones for 8th graders can be hard. Despite the fact that most of these students have probably never used a DVD, the DVD sleep screen phenomena is so pervasive that most generations are aware of it. As a refresher (students don’t need this), here’s the reference.Of course, one logo might work for graphing a single equation, initially, but for graphing systems, we’ll need two logos. So I generated a quick animation script to let students (1) enjoy a brain break and (2) give me qualitative descriptions of the logos’ behaviors (i.e., getting to the linear motion piece).
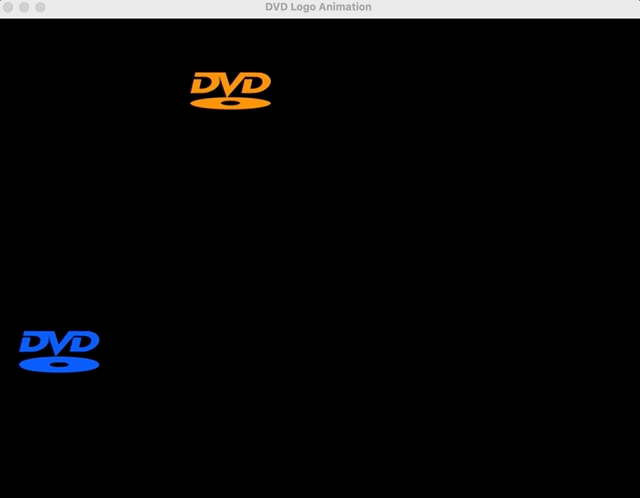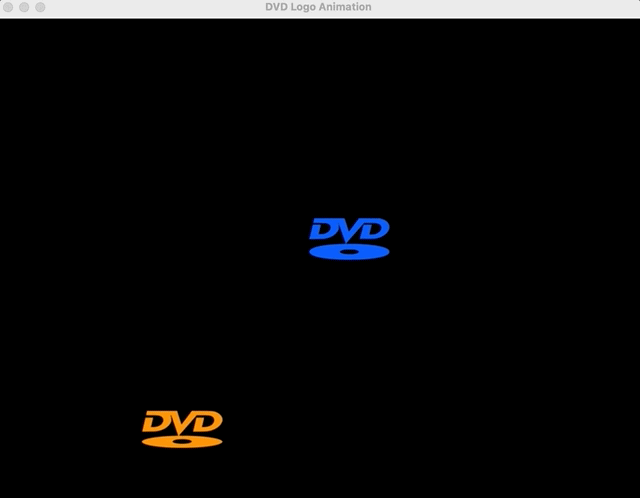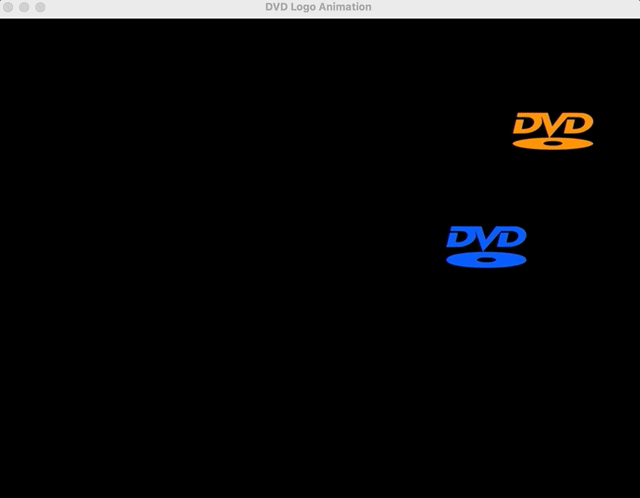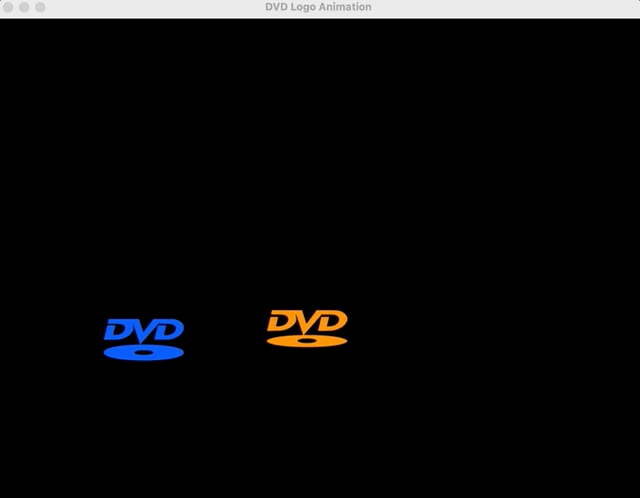
Instead of setting a goal of the logo hitting the corner, we can ask students if the logos will ever collide (a solution to our system of linear equations).
Grounding the Application in Today’s Lesson
Students will default to guesswork here, so it’s important to shift gears quickly and add mathematical precision to the exercise. To determine whether we’ll see a possible collision, graphing trajectories and looking for overlap (intersection, i.e., a solution) is the next obvious step (it’s okay to provide that insight).Pedagogical Note: A perceptive student might ask about the possibility for no collision despite path intersection (recognizing the time-series nature of the problem / velocity of the logos), but for the purposes of this lesson, it is not reasonable to extend the application any further.
We can demo a quick script to plot lines in the form $y=mx+b$ (with which our students are familiar given the bellringer warmup) and then animate the logos along their trajectories to look for collision.
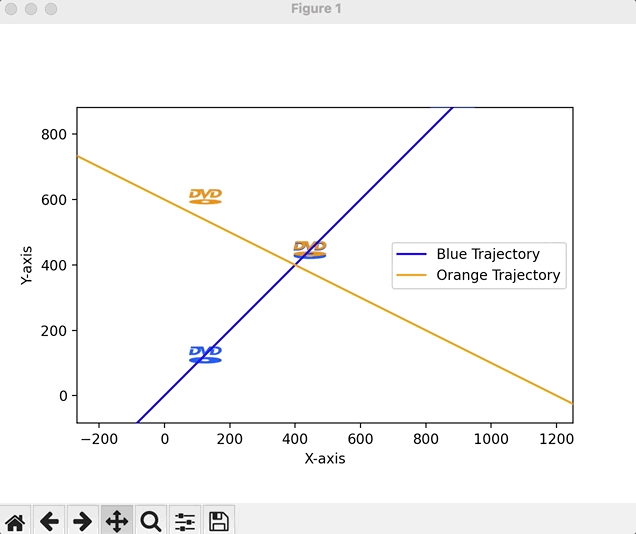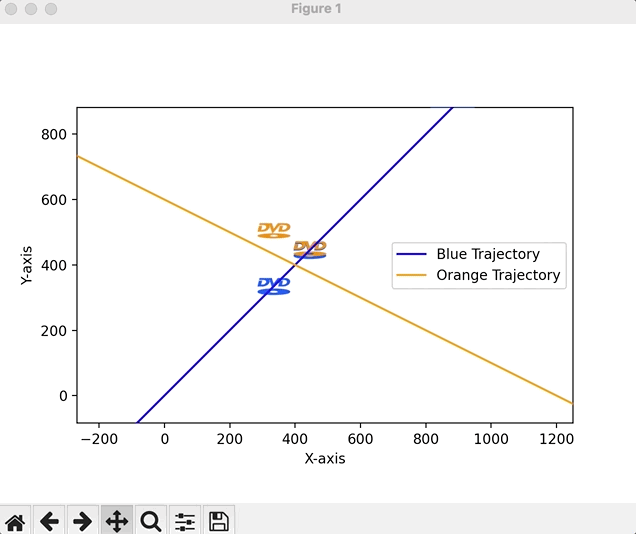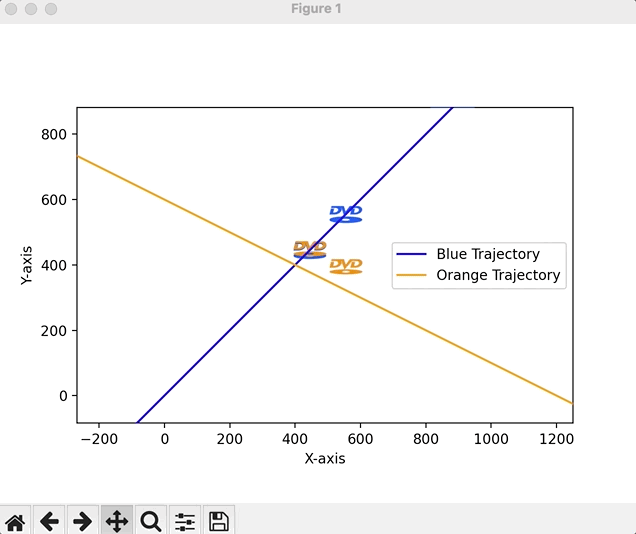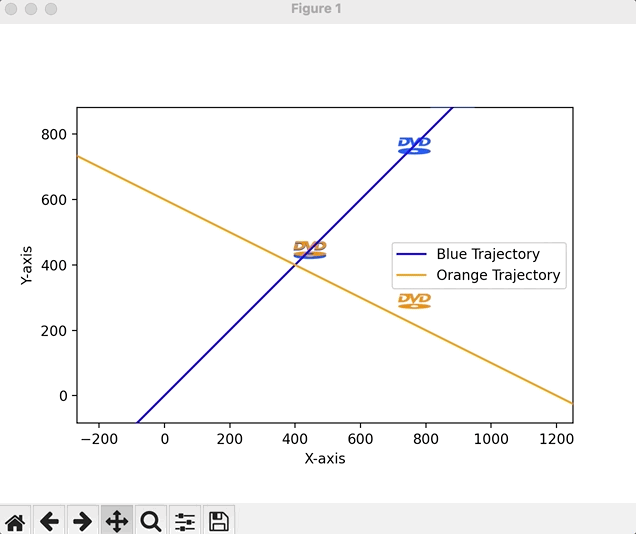
Students do not need any familiarity with the code, but it’s worth showing them the setup:
# Set line parameters for the first logo (blue)
m_blue, b_blue = 1, 0
# Set line parameters for the second logo (orange)
m_orange, b_orange = -0.5, 600They can immediately recognize $m$ (slope) and $b$ (y-intercept). Then you launch them into a group task: get me a slope and y-intercept that will prevent any collision from ever happening.
After a few minutes, test group candidate slopes/intercepts. Students will jump to wrong ideas like inverse slopes (1 and -1). The applet is wonderful for demonstrating that (maniacal laugh) they’re wrong! Slowly, they’ll converge to the idea of a shared slope and different intercepts, i.e., parallel lines $\rightarrow$ the case for an inconsistent system with no solution, no intersection, our goal for no collision!
Allow students (refrain from interrupting) to present the takeaways for their notes on their worksheet. I was surprised that they volunteered the idea of same slope, same intercept == infinite solutions (overlapping lines). We tested hypotheses of very close (yet different) y-intercepts which required much zooming on the applet to show the lines were, in fact, parallel, not the same line.
Overlapping (“Dependent”) Systems
I refrained from introducing the word “dependent” for the last exercise on the front page (because for most normal students, “dependent” will have better meaning in other contexts, not muddled by this Linear Algebra-driven definition ill-applied to Algebra 1). However, understanding systems where the other equation is a multiple of the first, is a must-have! Let students solve, plot, and describe the case of infinite solutions due to infinite “intersection.”Practice
Students can take this on their own or in groups. Have them underline (“find a solution”) in the directions so that they provide the ordered pair which satisfies both systems (if satisfiable).Students struggle with the final exercise (which makes for a good closer because they’ll desperately want the help). To help them come to the conclusion that $y=2$ is a horizontal line, ask them guiding questions:
- Is this equation in slope-intercept form? Many students will mistakenly say yes and apply a multiplier of 2 to each $x$ value despite it not being present at all in the equation.
- Once you (erroneously) conclude it’s not in slope-intercept form and impossible to get there, ask students to create a table. This is a fun opportunity to poke at students and try asking for different values of $x$, what is $y$? (It’s always 2! Make them read the statement then ask again and watch them get it wrong—you only get so many chances to ridicule students harmlessly, so take advantage of this.)
- Once they’ve filled in a table, they can graph and discover it’s a horizontal line.
- At risk of confusion, you can correct the earlier statement and tell them that it is possible to get to slope-intercept form (by using a coefficient of 0): $y=0x+2$
Then let them do a similar discovery for the other piece (vertical line).
That’s about it! Hopefully the takeaways are clear, the concepts are motivated via “real-world” applications, and the review is worthwhile. Godspeed and good luck!
Feel free to reach out for the code or other resources I built for 7th grade math standards.
Comments